Have you ever wondered why looking at a country map from the top looks so good with defined coastlines, yet when we are actually at a point on the edge, it really isn’t an edge rather a series of perturbances?
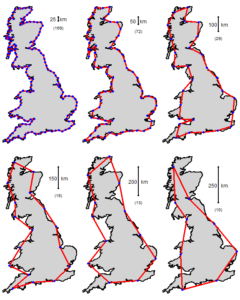
A question comes to mind, as to how exact is the length of the coast line then? Turns out, it depends on how smaller ruler one uses to measure the length of the coast, or what is the resolution of the map; the smaller scale would result in better estimation of coastline. But how small a scale could be, it might end up reaching to atomic scale then, a demonstration is shown in figure(1).
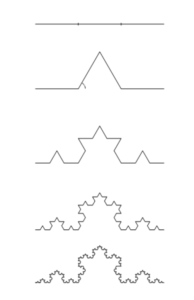
While not an important question for many, it gave rise to the concepts of Fractal geometry. A generalized understanding of this concept was developed by Mandelbrot from 1960s onwards. As per this theory, a pattern repeats itself number of times if we keep zooming on that surface, known as “”self-affinity”” of the surface (figure 2). A coastline or dendrites generated during solidification can be treated as fractal in a more general sense. This concept was put forwarded to explain surface roughness as well, Archard foreshadowed to this concept in 1957 [2] to explain why coefficient of friction is constant when force-area relationship is non-linear during contact.
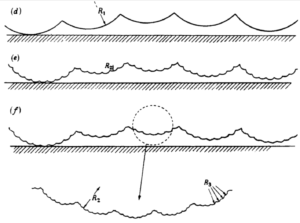
As per this modern understanding of fractal geometries, a spherical asperity on a surface is rather a combination of multiple spherical asperities if we zoom in further, and then further it would show asperities on that surface as well. As per this concept, surfaces were treated as exactly self-affine however, surfaces are only approximately self-affine i.e. the scale of magnification between horizontal and vertical dimensions varies by an exponential factor “”H””, known as Herst exponent. Thus, for Archard’s case, the Herst exponent would be 1.
Further complex surface contact models based on fractal theory have been developed by Bhushan Pawlus, McCool, Buchner, Persson etc. Interested readers are pointed to [3] for further development. An interesting demonstration of fractal geometry can also be seen in this video demonstrating Fractals which are not self-similar [4].
References:
[1] Gurung, Kris. (2017). Fractal Dimension in Architecture: An Exploration of Spatial Dimension.
[2] Archard J. F. (1957). Elastic deformation and the laws of frictionProc. R. Soc. Lond. A243190–205
[3] Barber, J.R. (2018). Contact of Rough Surfaces. In: Contact Mechanics. Solid Mechanics and Its Applications, vol 250. Springer, Cham.
[4] https://youtu.be/gB9n2gHsHN4

This article was written by Sallar Ali Qazi as part of an ongoing series of scientific communications written and curated by BioTrib’s Early Stage Researchers.
Sallar Ali Qazi is researching Mechanical and Tribo-Chemical Wear Modelling of Artificial Joint Prostheses at Imperial College London, UK